В декартовой системе координат уравнение прямой имеет такие виды:
Уравнение прямой с угловым коэффициентом
Explicit equation of straight line / slope – intercept form
\(y=k\cdot x + b\), где:\(k\) – угловой коэффициент (slope), \(k = tan(\alpha)\)
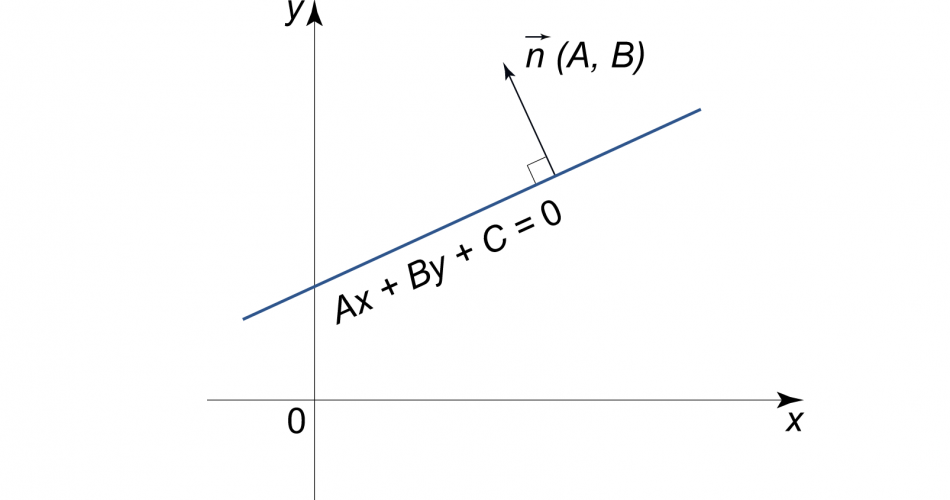
Общие уравнение прямой
General equation of a straight line
\(A\cdot x + B\cdot y + C = 0\)- вектор нормали (Normal Vector): \(\vec{n}=(A,B)\)
- Угол прямой (slope of straight line):
\(k = tan(\alpha) = \frac{y_2 – y_1}{x_2 – x_1}\) - Если С = 0, то \(A\cdot x + B\cdot y = 0 => y = -\frac{A}{B}\cdot x \),
если \(k = -\frac{A}{B}\), то прямая будет проходить через начало координат - Если B = 0, то \(A\cdot x + C = 0 => x = -\frac{A}{C}\), прямая паралельна оси Oy
- Если A = 0, то \(B\cdot y + C = 0 => y = -\frac{B}{C}\), прямая паралельна оси Ox
Уравнение прямой через угол и точку
Equation of a straight line given a point and slope (point-slope form)
\(y = y_0 + k\cdot(x – x_0)\)
Прямая через две точки
Equation of a straight line passing through two points (two-points form)
\(\frac{y – y_1}{y_2 – y_1} = \frac{x – x_1}{x_2 – x_1}\)или
\( \begin{bmatrix}x & y & 1 \\
x_1 & y_1 & 1 \\
x_2 & y_2 & 1 \\
\end{bmatrix} = 0
\)

Уравнение прямой в отрезках на осях
Intercept form of a straight line equation
\(\frac{x}{a} + \frac{y}{b} = 1\), гдеa – величина отрезка которая отсекает прямую на оси Ox
b – величина отрезка которая отсекает прямую на оси Oy

Нормальная форма уравнения прямой
Normal form of a straight line equation
\(x\cdot cos\beta + y\cdot sin\beta – p = 0\), где параметр p равен дистанции между прямой и началом координат
Уравнение прямой через вектор и точку
Point direction form of a straight line equation
\(\frac{x – x_1}{m} = \frac{y – y_1}{n}\)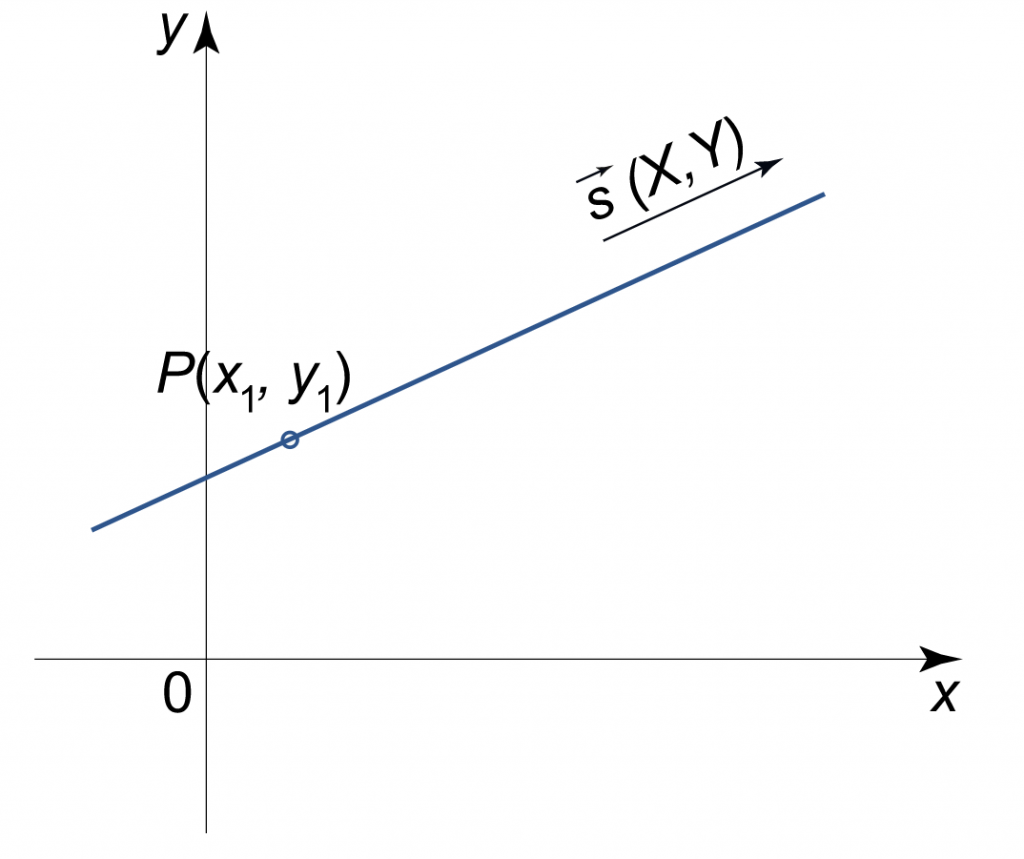
Дистанция от точки до линии
Distance from a point to a straight line
\(d = \frac{|Ax_1 + By_1 + C|}{\sqrt{A^2 + B^2}}\)
Параллельные линии
Parallel line
Прямые \(y = k_1\cdot x +b_1\) и \(y = k_2\cdot x +b_2\) параллельны если \(k_1 = k_2\)

Перпендикулярные линии
Perpendicular line
Прямые \(y = k_1\cdot x +b_1\) и \(y = k_2\cdot x +b_2\) перпендикулярные если \(k_1 = -\frac{1}{k_2}\) или \(k_1 \cdot k_2 = -1\). Обозначают перепендукулярность \(\bot\)

Угол между прямыми
Angel between straight lines
\(tg\alpha = \frac{k_2 – k_1}{1 + k_1\cdot k_2}\)Если уравнения заданы в общей форме:
\(cos\alpha = \frac{A_1\cdot A_2 + B_1\cdot B_2}{\sqrt{A_1^2 + B_1^2}\cdot\sqrt{A_2^2 + B_2^2}}\)

Точка пересечений двух линий
Intersection of two lines
\( \begin{cases}A_1\cdot x + B_1\cdot y + C_1 = 0 \\
A_2\cdot x + B_2\cdot y + C_2 = 0
\end{cases}\)
Координаты находятся как:
\(x = \frac{\Delta_x}{\Delta}\)
\(y = \frac{\Delta_y}{\Delta}\)
где:
\(
\Delta = \begin{bmatrix}
A_1 & B_1 \\
A_2 & B_2 \\
\end{bmatrix};
\)
\(
\Delta_x = \begin{bmatrix}
-C_1 & B_1 \\
-C_2 & B_2 \\
\end{bmatrix};
\)
\(
\Delta_y = \begin{bmatrix}
A_1 & -C_1 \\
A_2 & -C_2 \\
\end{bmatrix};
\)